De mémoire (mon grand intérêt pour ces unités date de presque dix ans) la masse de Planck était tout simplement la plus grand masse possible pour un photon et donc la masse qu'aurait un photon dont la longueur d'onde serait la longueur de Planck soit (de mémoire) environ 10 puissance moins 35 mètres.....
Cela étant relié au temps de Planck qui serait la plus petite durée (1/10^44 seconde) et donc l'inverse de la plus grande fréquence (10^44 hz) ..... qui serait donc celle de ce fameux photon maximal.
A mon avis, la seule piste réellement utile est celle que je tente par périodes (pas en ce moment) de creuser depuis 15 ans : QUANTIFIER LE PHOTON LUI-MEME....
Non pas faire ce qui est déjà fait E = N * h nu avec N entier qui est le NOMBRE ENTIER de PHOTONS dans un flux lumineux.....
Mais de chercher de COMBIEN d'UNITES d'ENERGIE ELEMENTAIRE est fait UN SEUL PHOTON.....
En tigonnant les lois des niveaux d'énergie, on voit bien apparaître une telle logique qui montrerait que le PHOTON VIOLET contiendrait DEUX FOIS PLUS d'ATOMOS - de corpuscules de base - que le PHOTON ROUGE.... et que l'énergie de chaque photon serait donc PROPORTIONNELLE à la QUANTITE (entière) d'ATOMOS que ce photon contient....
Je n'ai jamais pu avoir ce débat avec les "ortohodoxes" à cause de leur OBSTINATION ABSURDE à refuser de donner une masse aux photons.... (pour protéger la stupide fonction gamma de Einstein qui fait ralentir le temps)
Si Louis De Broglie était vivant (je lisais sa préface de 1973 (Flammarion 1986*) hier dans un livre que j'ai acheté dimanche sur un marché.... 2 euros)... je lui écrirais en sachant qu'il serait 1000 fois plus OUVERT QUE LES PRESOMPTUEUX RELATIVISTES qui contrôlent les structures de recherche...
A l'APPROCHE DE LA MORT, DE BROGLIE RECUSAIT TOUTES LES ÂNERIES DE BOHR qu'il avait GOBEES (et professées) PENDANT DES ANNEES....
Idem pour Georges Lochak qui préface l'ouvrage
Louis de Broglie La physique nouvelle et les quanta. 1937 1973
La formule de Johann Balmer généralisée est la clé :
 elle permet de supposer qu'un photon s'introduit dans l'électron, que celui-ci change d'orbite. Puis qu'un 2° photon le rejoint. De supposer que les deux photons fusionnent en un seul. Formé de la somme des atomos avec une énergie totale somme de l'énergie des deux photons..... Et que le départ de ce photon unique aboutirait au retour de l'électron sur le rayon de Bohr....
elle permet de supposer qu'un photon s'introduit dans l'électron, que celui-ci change d'orbite. Puis qu'un 2° photon le rejoint. De supposer que les deux photons fusionnent en un seul. Formé de la somme des atomos avec une énergie totale somme de l'énergie des deux photons..... Et que le départ de ce photon unique aboutirait au retour de l'électron sur le rayon de Bohr....LIRE WIKIPEDIA qui ne décrit pas cela..... mais donne les formules qui en sont compatibles
Aspects expérimentaux et historiqueAu cours du XIXème l'amélioration des techniques de l'optique (notamment avec l'usage des réseaux plans) permet le développement de la spectroscopie. Dès 1859 Kirchhoff et Bunsen découvrent que les raies spectrales des éléments chimiques sont caractéristiques de ceux-ci. Cette technique permettra la découverte de nombreux nouveaux éléments parmi lesquels le césium (en 1860), le rubidium (en 1861) et surtout l'hélium en 1868 par Janssen et Lockyer.
En 1885 Balmer découvre que les longueurs d'onde des 4 raies d'émission dans le visible de l'hydrogène, identifiées peu avant par Angström comme étant situées respectivement à 656,3 nm, 486,1 nm, 434,0 nm et 410,2 nm, sont données par la formule empirique suivante, dite de Balmer:avec
,
avec(valeur moderne), dite constante de Rydberg de l'atome d'hydrogène. Cette formule, dite de Balmer, est rapidement généralisée par Rydberg et Ritz à la suite de la découverte de nouvelles « séries » de raies dans d'autres domaines du spectre, sous la forme suivante, dite de Rydberg-Ritz:
avec
.
Dans cette formule, dite de Rydberg-Ritz, p est l'indice de la série, et n l'indice de la raie. La formule de Balmer correspond à la série p=2 (cette série est ainsi nommée "série de Balmer"). Différentes séries convergentes de raies seront progressivement mises en évidence dans le spectre de l'atome d'hydrogène:
: série de Lyman, dans l'ultraviolet;
Parallèlement, la formule de Rydberg-Ritz est généralisée à d'autres éléments que l'hydrogène, notamment les ions dithydrogénoïdes et certains alcalins, au prix d'une modification de la constante de Rydberg, et l'utilisation de nombres non-entiers pour l'indice de raies ("correction de Rydberg3").
: série de Paschen, dans l'infrarouge proche;
Dans le même temps, l'existence même de spectres de raies plutôt que de spectres continus n'est pas alors expliquée par la théorie classique, et posera un problème dès le début de l'essor des théories sur la structure de l'atome. En effet, l'expérience de Rutherford montre en 1911 que l'atome est constitué d'un noyau positivement chargé, concentrant l'essentiel de la masse dans un rayon environ 100000 fois plus petit que l'atome lui-même, et d'électrons négativement chargés "en orbite" autour de ce noyau sous l'action de l'interaction électrostatique. Si l'origine de l'émission ou l'absorption de radiations électromagnétiques par les électrons peuvent facilement se comprendre dans le cadre de la théorie classique de l'électromagnétisme, une difficulté de taille apparaît. En effet, la théorie prévoit naturellement que les spectres doivent être continus et non pas de raies. Elle est bien sûr par suite impuissante à expliquer les régularités dans certains spectres mis en évidence par les formules (1) et (2).
Au demeurant, l'existence même de l'atome ne peut être expliquée par la théorie classique: l'électron étant accéléré dans le champ du noyau, les équations de Maxwell prédisent qu'il doit rayonner de l'énergie et finir par "s'écraser" sur le noyau.
En 1913, Niels Bohr propose un modèle empirique permettant de rendre compte de la stabilité de l'atome d'hydrogène et de l'existence des raies de son spectre. Dans ce modèle (cf. atome de Bohr pour plus de détails), l'électron est en interaction électrostatique avec le noyau, supposé infiniment lourd, et se dépace sur des orbites circulaires de rayon r similaires à celles des planètes autour du Soleil (cf. problème à deux corps). Toutefois Bohr, s'inspirant de la théorie naissante dites des quanta, postule que les seules orbites permises sont celles pour lesquelles le moment cinétique de l'électron sont quantifiées, avec la condition suivante:(me étant la masse de l'électron) avec n entier strictement positif. Sur de telles orbites il est postulé que l'électron ne rayonne pas d'énergie. Les différentes orbites admissibles ont donc des rayons quantifiées donnés par
avec
et
rayon de Bohr de l'atome d'hydrogène, de valeur environ 53 pm.Cette condition implique une quantification de l'énergie de l'électron qui s'écrit alors sous la forme
avec
énergie d'ionisation de l'atome (e est la charge élémentaire). Dans ce contexte l'émission ou l'absorption de lumière est expliquée par Bohr comme le passage d'une orbite d'énergie supérieure (resp. inférieure) Ep à une autre d'énergie inférieure En avec n>p(resp. supérieure), la longueur d'onde de la lumière émise étant alors donnée par la formule d'Einstein comme liée à la différence d'énergie entre les deux orbites:
, d'où pour le nombre d'onde de la transition
.
On retrouve ainsi la formule de Rydberg-Ritz (2), en identifiantet
, ce qui est vérifié par le calcul qui donne en effet
avec la formule précédente et bien sûr
.
Si la théorie de Bohr permet d'expliquer la formule de Rydberg-Ritz, et l'existence de spectres de raies pour les atomes, elle le fait au prix d'une hypothèse ad hoc difficilement conciliable avec la théorie classique. Si l'expérience de Franck et Hertz apporte dès 1914 une confirmation expérimentale du modèle de Bohr, et malgré l'amélioration de celui-ci parSommerfeld pour tenir compte d'orbites elliptiques, et expliquer en partie l'existence de la structure fine du spectre de l'atome d'hydrogène mise en évidence expérimentalement, les difficultés conceptuelles demeurent et ne seront résolues qu'avec le développement de la mécanique quantique dans les années qui suivront. L'atome d'hydrogène est aujourd'hui celui pour lequel la théorie quantique arrive à décrire le spectre avec la plus grande précision, en plein accord avec l’expérience. Son étude est indispensable pour aborder la théorie des atomes à plusieurs électrons ainsi que celles desmolécules, en permettant d'introduire de nombreux concepts fondamentaux en physique atomique et en chimie (cfatomistique), en particulier la notion centrale d'orbitale atomique.
Description générale de l'atome d'hydrogèneL'atome d'hydrogène est constitué d'un noyau comprenant un seul proton de masse= 1,672 65.10-27 kg et de charge
, et d'un électron de masse
= 9,109 53.10-31 kg et de charge
,
étant la charge élémentaire:
= 1,602 189.10-19 C. Le proton comme l'électron sont des fermions de spins respectifs notés
(spin nucléaire) et
(spin électronique), de même valeur
.

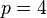 et
et 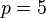 , séries de
, séries de
Aucun commentaire:
Enregistrer un commentaire